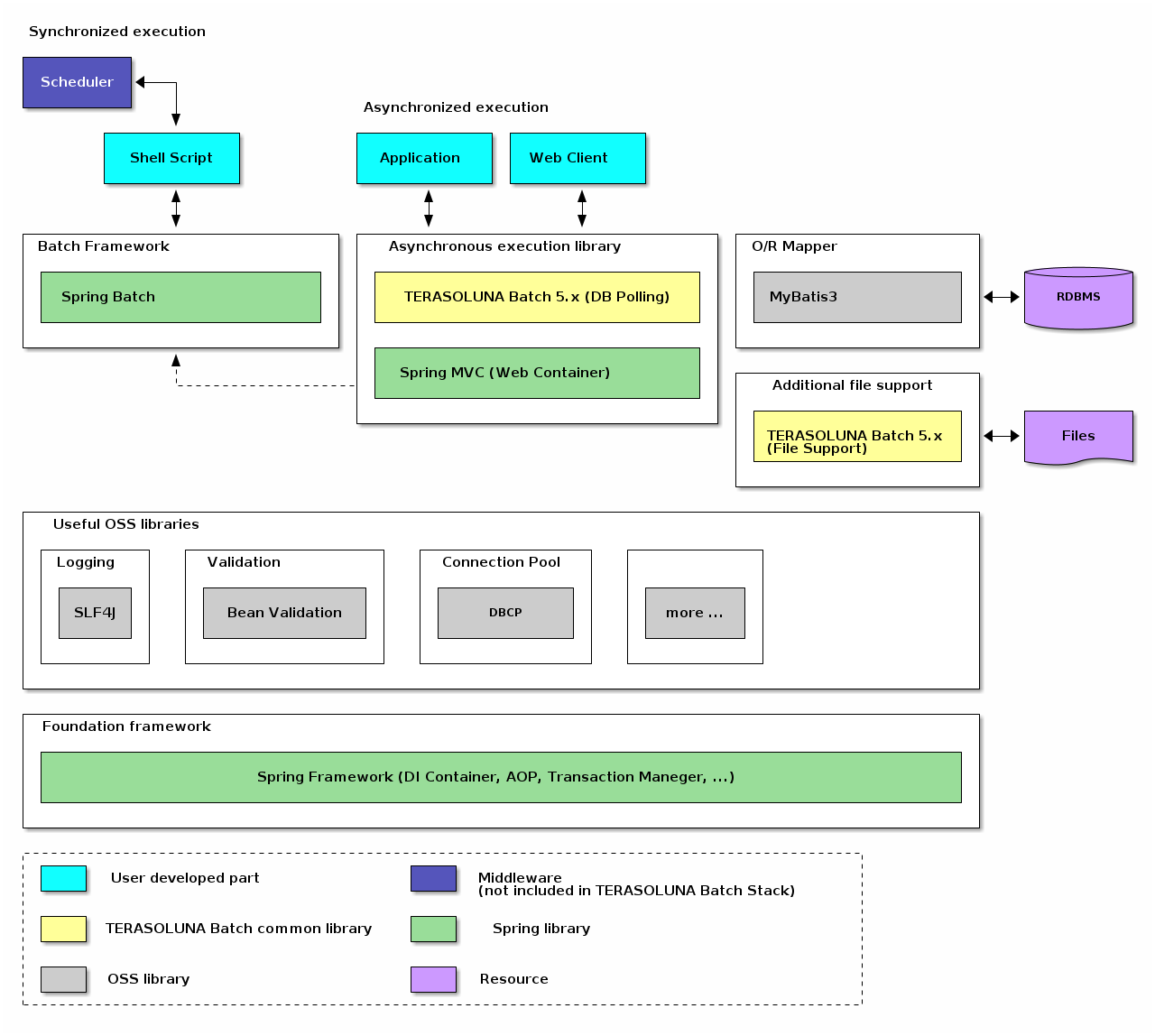
Terasoluna Batch Framework For Java 5 X Development Guideline
平行線の同位角と錯角の性質 ここでは中学生の数学で出てくる、 平行線の同位角(どういかく)と錯角(さっかく)の性質について 確認しておきたいと思います。 この公式のポイント お互いの意見が対立し、その状態が継続する時、 「平行線を辿る」 という言葉を使ってみましょう。 このような時は、場の雰囲気を変えるため、食事の時間を取ったり、休憩時間を設
平行線の性質とは
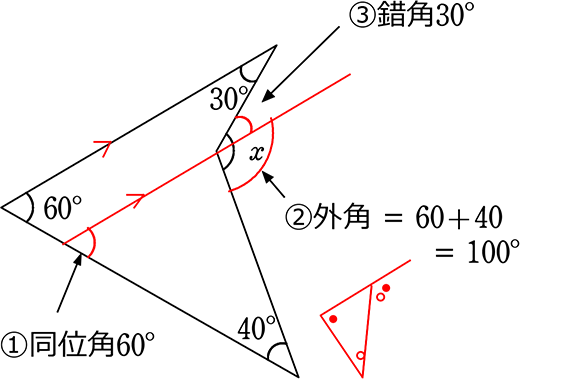
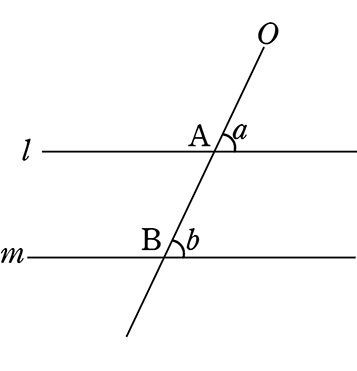
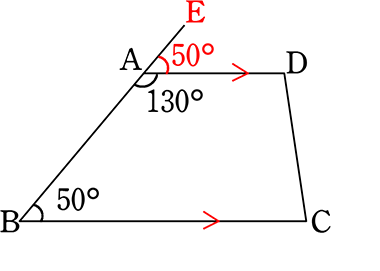
平行線の性質とは-平行線 は 様々なヒントを与えてくれる特別な存在 だよ。 2つの直線が平行なとき、どんなことが言えるかを、計2回の授業でおさらいしていくよ。 2直線が平行なときの「同位角」「錯角」の性質 ま 平行線という言葉・・・ ただの位置関係しか示せなかった同位角が、証明のエースに化ける魔法の言葉です。 l と m は平行な直線です。 この場合、∠ a と∠ b の角の大きさは等しくな

平行線と線分の比 Ict教材eboard イーボード
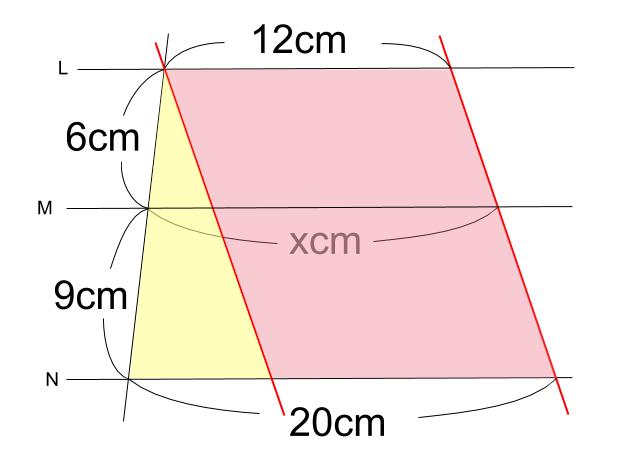
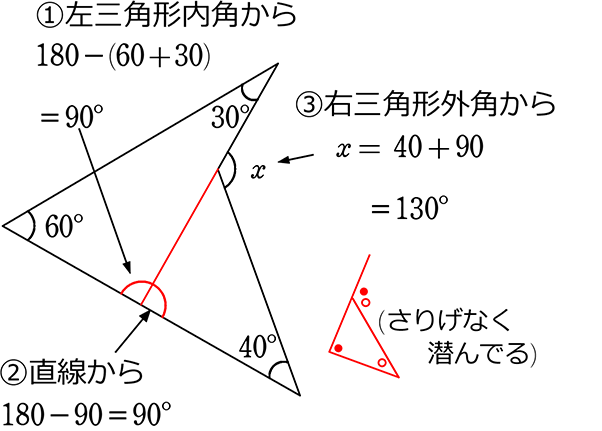
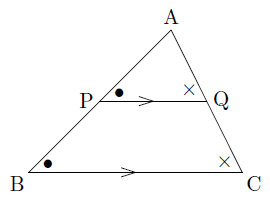
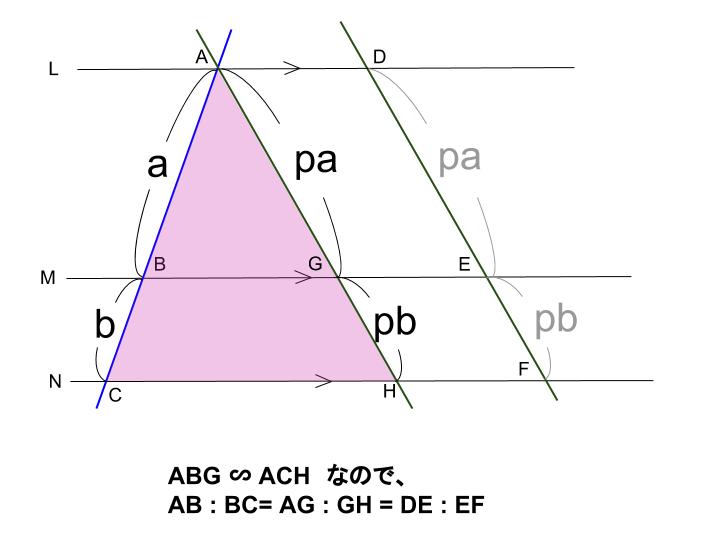
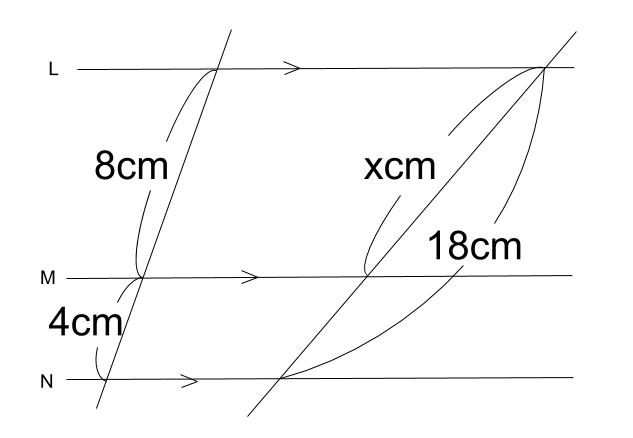
解説 ①と②で似たような図です。 もちろんどちらも似たような解き方で解けます。 どちらも、「相似」や「平行線と線分の比」の利用で解きます。 ただし・・・ ①をいわゆる「公式」で習った 角と平行線のまとめ ・対頂角 2本の直線が交わってできる 向かい合った2つの角 (対頂角は等しい) ・同位角 2本の直線と1本の直線が交わる時 「同じ位置」にある2つの角のこと ・図1 平行線と線分の比 右図2のような図形において幾つかの辺の長さが分かっているとき,未知の辺の長さを求めるために図1の黄色の矢印に沿って辺の長さを求めることができる. BD//CE のとき
平行度の記号 平行度の記号は、傾いた2本の平行線 です。 平行度の図示方法 ここでは面と面の平行度の図示方法を紹介します。 下の図は、データム平面aに対して、反対面に平行度を指示した図面デジタル大辞泉 平行線の用語解説 1 同一平面上にあって、どこまで延長しても交わらない2本またはそれ以上の直線。2 互いの主張・意見などがどこまでいっても妥協点の見いだせない状態をいう平行線公準 (へいこうせんこうじゅん)とは、 ユークリッド幾何学 における特色のある 公準 である。 平行線公理 、 ユークリッド原論 における5番目の公準であったことから、 ユークリッド(エ
平行線の性質とはのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
/assets/images/4149160/original/b5b8e9fa-96e4-49db-870d-a2b5a392217e?1570005918) 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 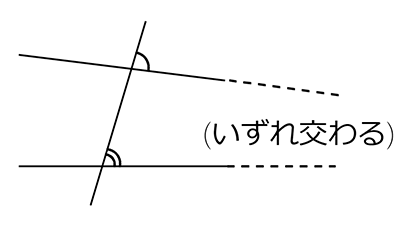 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 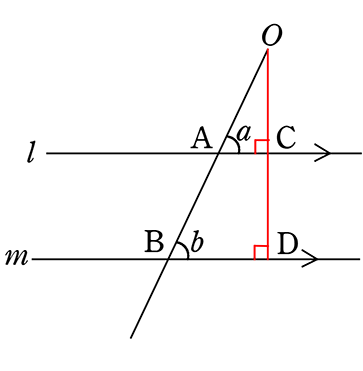 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 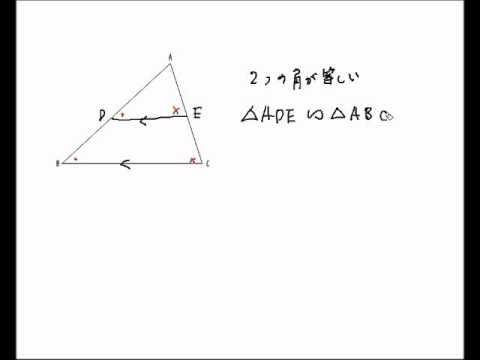 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 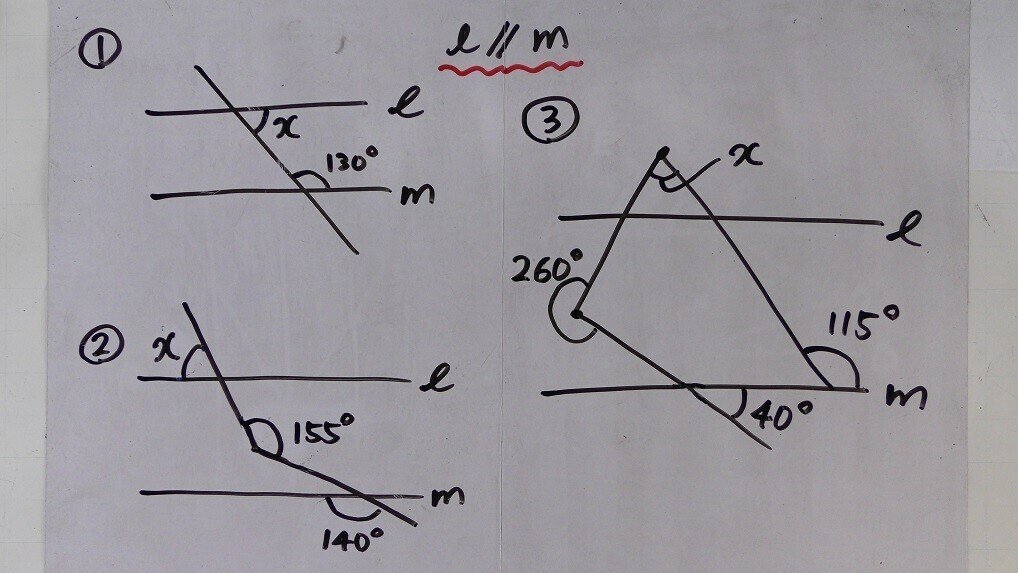 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 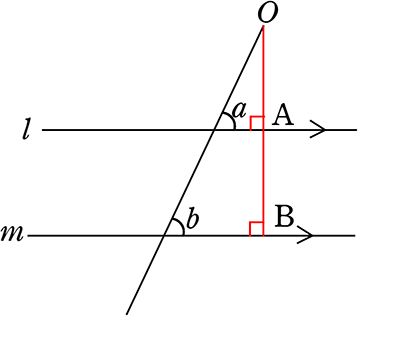 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 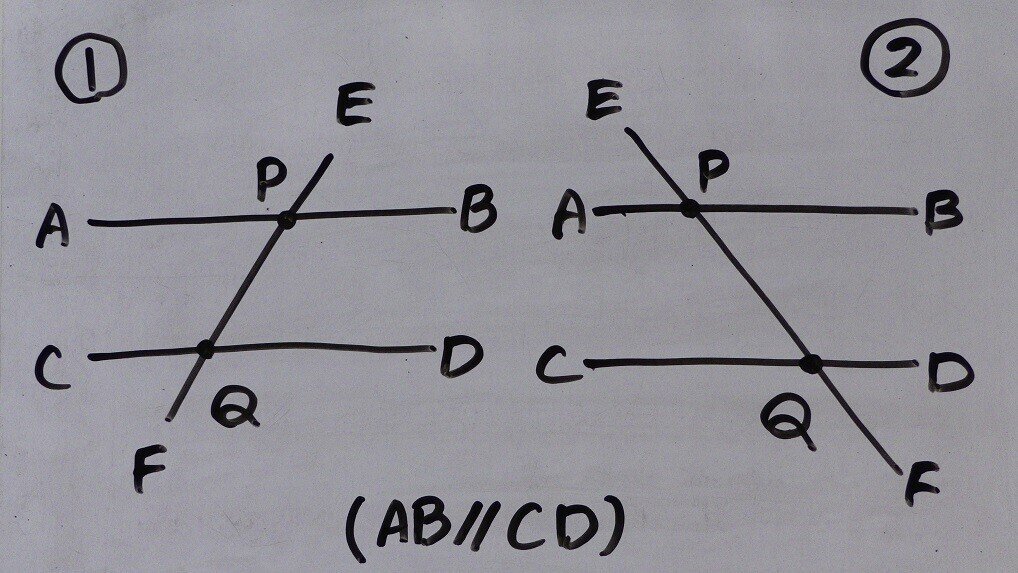 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 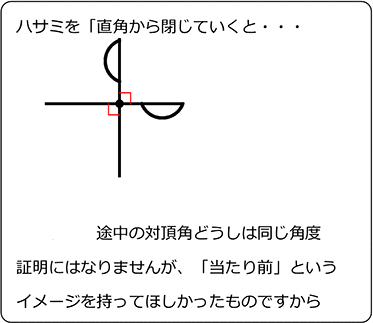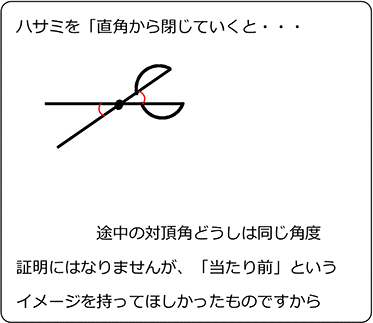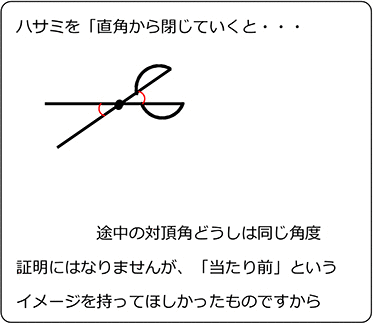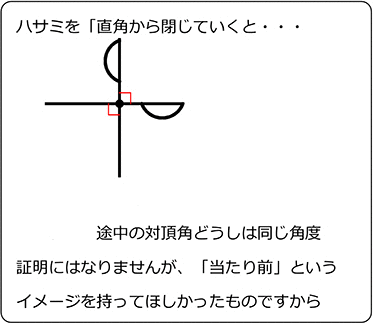 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 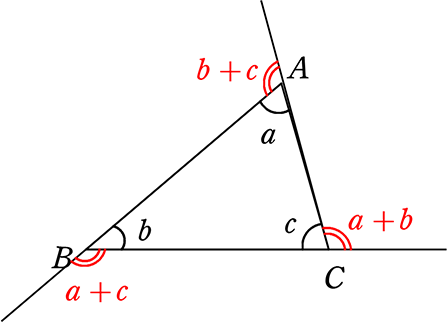 平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 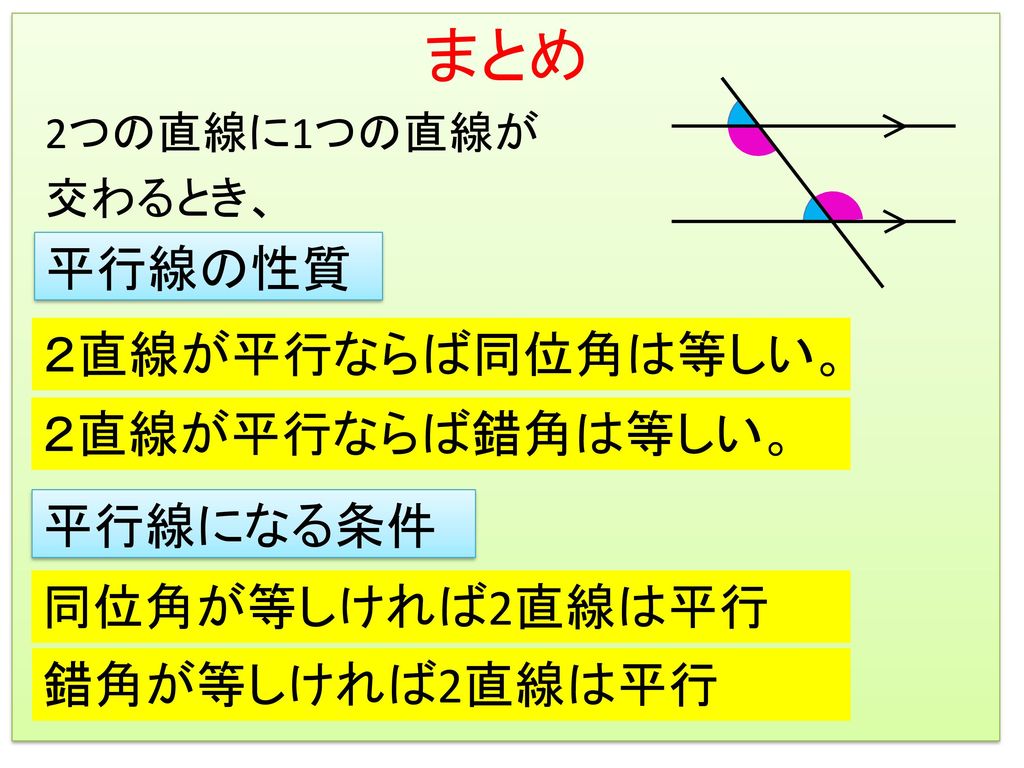 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 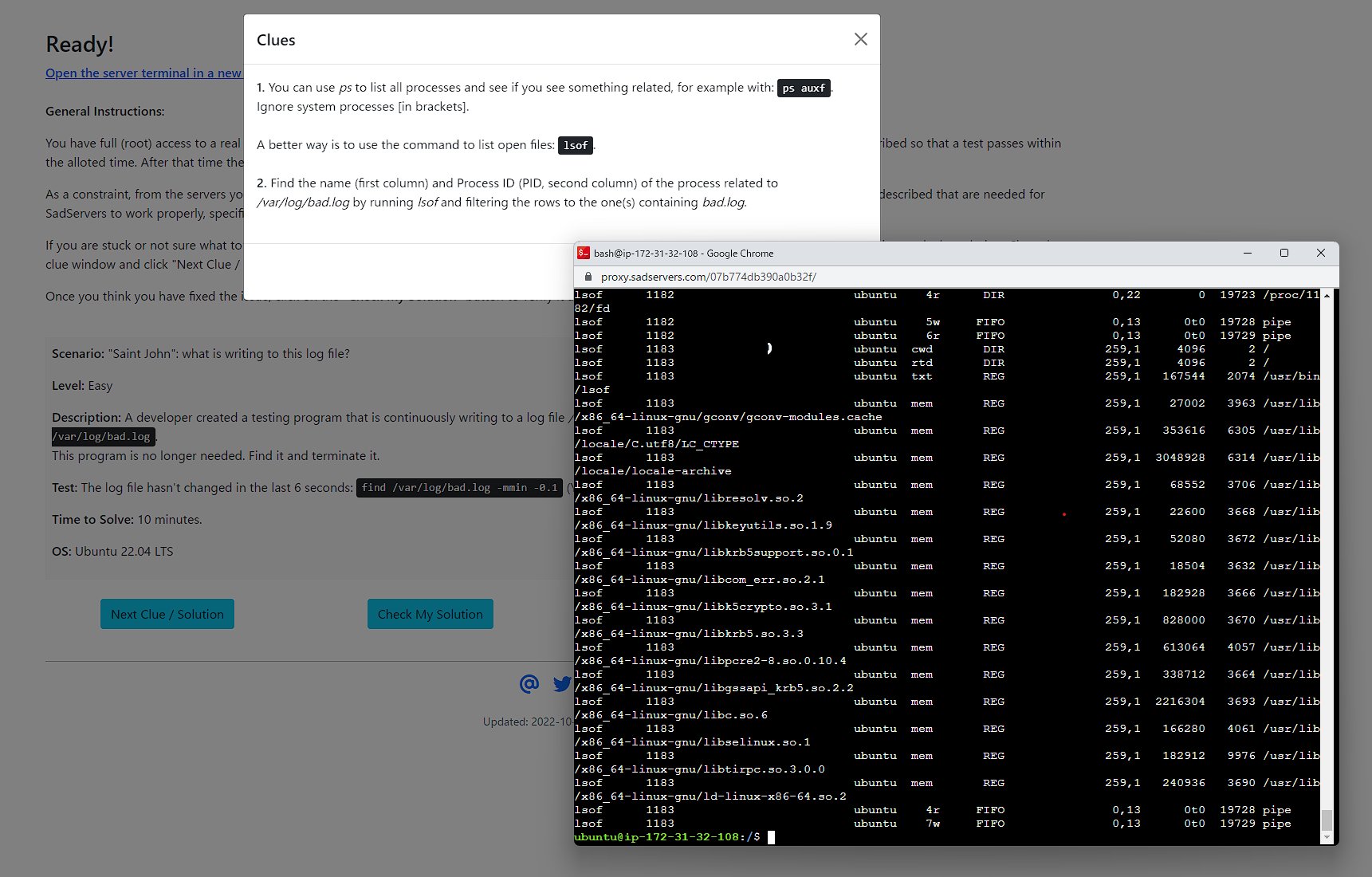 平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント | 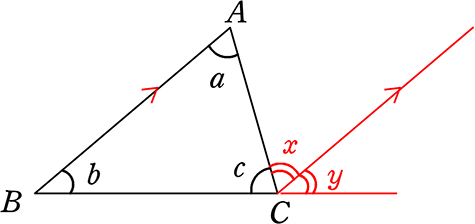 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント | 平行線と線分の比 無料で使える中学学習プリント |
「平行線の性質とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |  平行線と線分の比 無料で使える中学学習プリント |
 平行線と線分の比 無料で使える中学学習プリント | 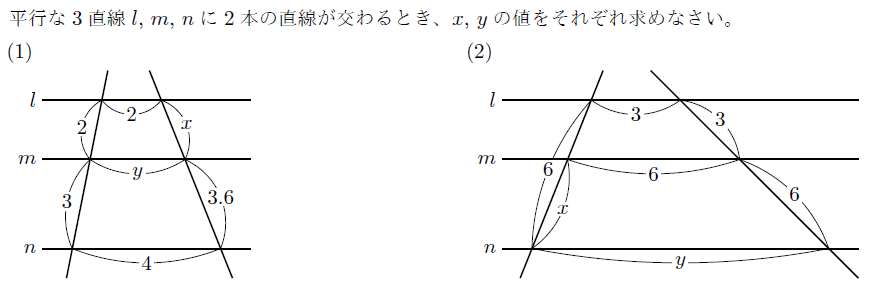 平行線と線分の比 無料で使える中学学習プリント |
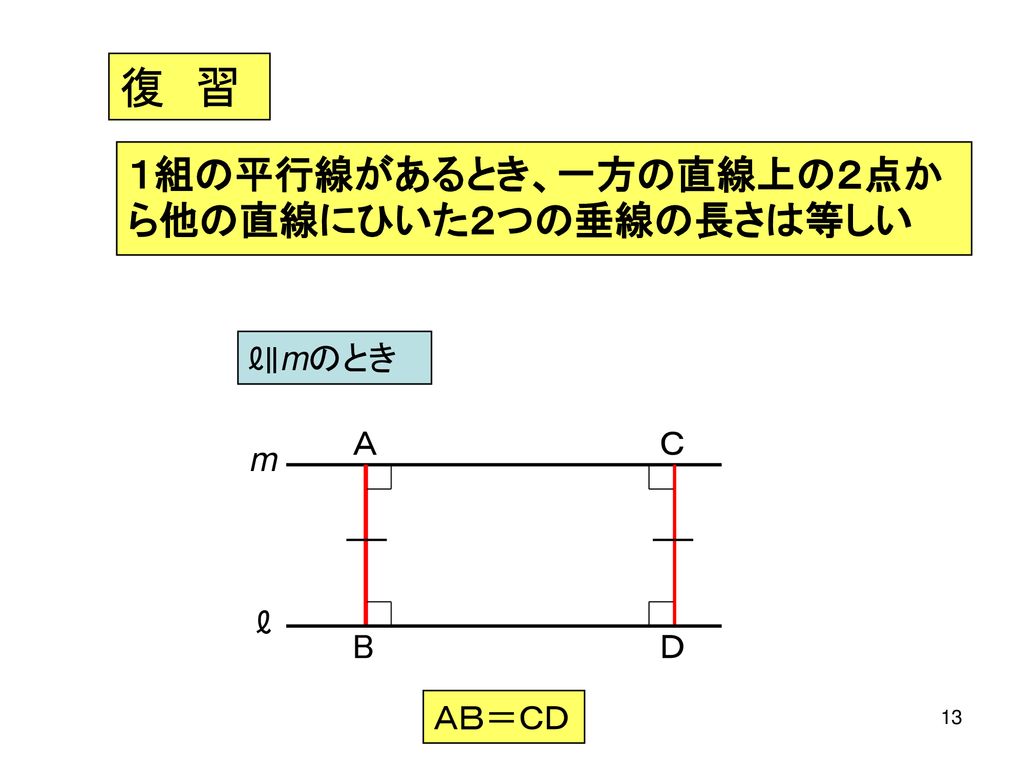
平行とは 同一の平面上にあって、 両方向に限りなく延長しても、 いずれの方向においても互いに交わらない直線 ・ (数学的証明) Oから直線lとその平行線mに 垂線 を下す (三角形の内角の和は180°) 2つの平行な直線について、 同位角は等しい(公準) 錯角が等しい という性質があります 。 実はこの逆、2つの(平行かはわからない)直線があって 同位角が等しい 錯角が等しい の
Incoming Term: 平行線の性質とは,




0 件のコメント:
コメントを投稿